
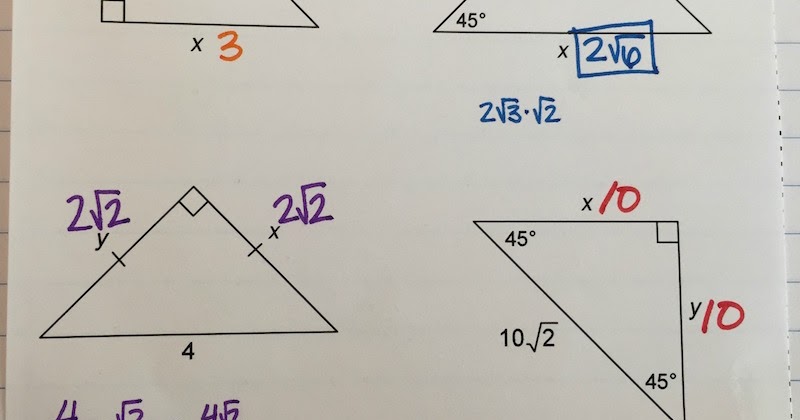
You reinforce similarity in a seemingly easy scenario, you get some number sense in, and you can extend to more cases. With the use of calculators you'll get students definitely agreeing that the long leg is. So I say take squares, cut them in half- take equilateral triangles, cut them in half- and measure side ratios. For example, if they solve for the long leg of 30-60-90 and get sqrt(3)/2 how do they know that they are right? Sure they can test it with the pythagorean theorem, but that's going to rely on their use of the same skills of the ones they are checking - instead of building on a foundation skill they are more comfortable with. Even if students can do the pythagorean derivation of the sides, there are frequent errors since their number sense with fractions and radicals is low, or the "too just so" 1-1-sqrt(2) ratio trips them up. You can still start with the square and the equilateral triangle and measure them with approximate decimals instead of the radicals. Let me try to explain better what I mean because I believe we are mostly on the same page.
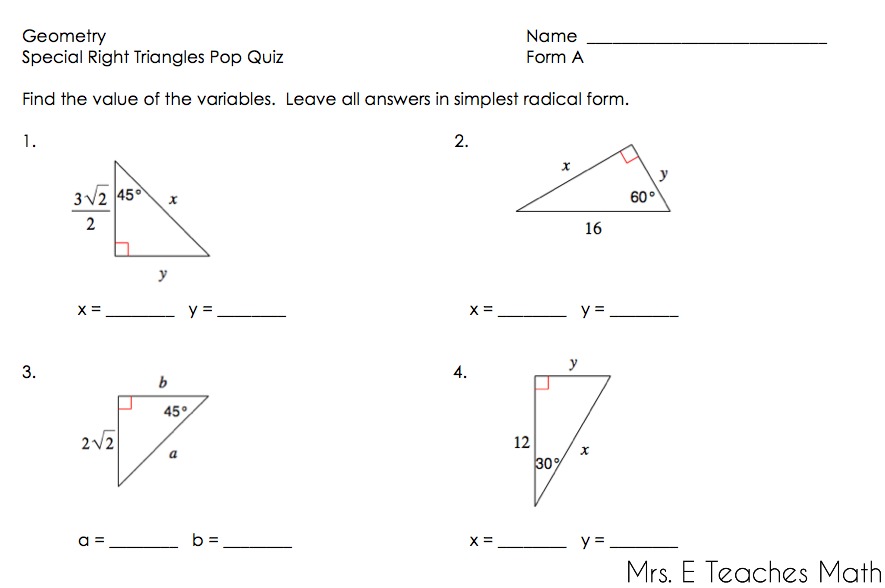
And you are also right that relying on memorization is useless. You are right that the natural revelation of this concept is from half of the square and half of the equilateral triangle. Oh certainly I don't mean to pull the numbers out of nowhere. Lots of contextual stuff you can do before you get very direct about how special the special right triangles are. And those ratios of angles are found in the triangles formed by diagonals in the regular pentagon. 1,1,3 and 1,2,2 are the only unique unordered 3-partitions of 5. Where's the x,x,5x angled triangle? how about x,2x,2x ? Notice how this exploration can pair with the number theory exercise of partitions. but don't skip the 1,1,sqrt(3) side lengthed triangle with angles of x,x,4x (30,30,120) Or go to the hexagon and find all the equilateral triangles. Its not half, but draw one of the diagonals in the pentagon and you have the golden ratio, (1+sqrt(5))/2 also forming the x,x,3x triangle (36, 36, 108) which can relate to the x,x,2x (45-45-90) and the x,2x,3x (30-60-90) If the 30-60-90 is half of the equilateral triangle,Īnd the 45-45-90 is half of the square.Īre there interesting triangles from the regular pentagon? (yes) (in Harel's sense of intellectual need.)Īlso you can expand upon the context for these triangles by talking about more "special triangles" as parts of regular polygons: then you reveal the big relief: sqrt(2) is a succinct way of getting exactly the right ratio. 866a, 1a Not only is it useful that students are familiar with the approximations, it helps them get the "triangle idea" without struggling with the "radical idea". a 45-45-90 triangle has approximate side ratios of a, a, 1.414a (or. I never got around to trying this with the whole class (I did it for individuals sometimes) it but you could start by doing special right triangles with the decimal approximations. Consider: how much time have they REALLY had to work with these numbers? a couple weeks in algebra? A few things here and there in middle school? Probably less than a month of their lives before this and we expect them to handle it no problem. sqrt(2) and sqrt(3) look more like blahrg and erggbl to them. It could be they struggle with this because they don't recognize square roots as familiar or useful numbers.


 0 kommentar(er)
0 kommentar(er)
